Teleport Blog - Comparing SSH Keys - RSA, DSA, ECDSA, or EdDSA? - Apr 7, 2022
Comparing SSH Keys - RSA, DSA, ECDSA, or EdDSA?
This blog post was originally released on 08/26/20.
Seeking a broader overview? Start here: What is Cryptographic Identity?
What’s worse than an unsafe private key? An unsafe public key.
The “secure” in secure shell comes from the combination of hashing, symmetric encryption, and asymmetric encryption. Together, SSH uses cryptographic primitives to safely connect clients and servers. In the 25 years since its founding, computing power and speeds in accordance with Moore’s Law have necessitated increasingly complicated low-level algorithms. This article will focus on asymmetric keygen algorithms.
As of 2020, the most widely adopted algorithms are RSA, DSA, ECDSA, and EdDSA, but it is RSA and EdDSA that provide the best security and performance.
Encryption Within the SSH Protocol
SSH is used almost universally to connect to shells on remote machines. The most important part of an SSH session is establishing a secure connection. This happens in two broad steps:
- Negotiation & Connection
- Authentication
Negotiation & Connection
In order for an SSH session to work, both client and server must support the same version of the SSH protocol. Modern clients will support SSH 2.0, as SSH 1.0 has identified flaws. After coming to a consensus on which protocol version to follow, both machines negotiate a per-session symmetric key to encrypt the connection from the outside. Generating a symmetric key at this stage, when paired with the asymmetric keys in authentication, prevents the entire session from being compromised if a key is revealed. Negotiation terms happen through the Diffie-Helman key exchange, which creates a shared secret key to secure the whole data stream by combining the private key of one party with the public key of the other. These keys are different from the SSH keys used for authentication. For those interested in learning more about this step, this comprehensive article, SSH Handshake Explained, is a great starting point.
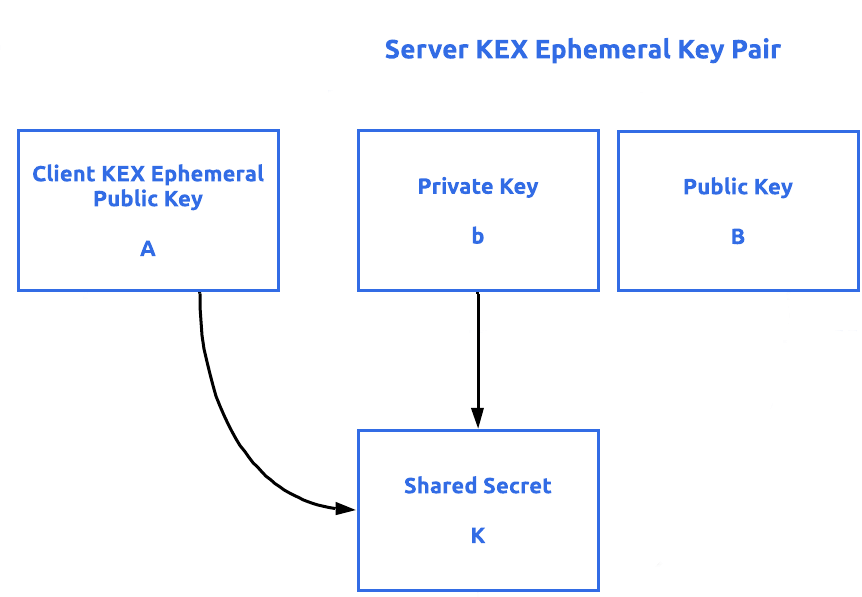

Authentication
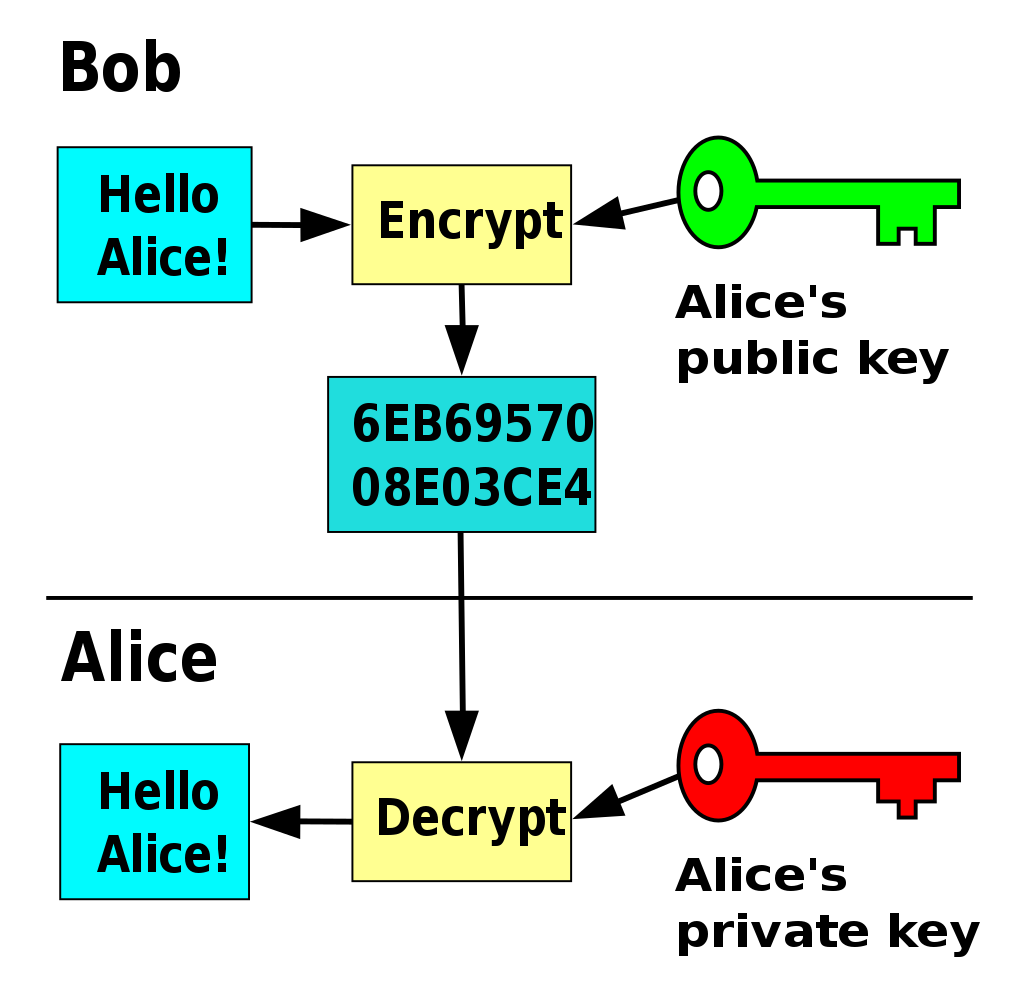
After completing the negotiation and connection, a reliable and secure channel between the client and server has been established. During the KEX, the client has authenticated the server, but the server has not yet authenticated the client. In most cases, public-key authentication is used by the client. This method involves two keys, a public and private key. Either can be used to encrypt a message, but the other must be used to decrypt. This is what is meant by asymmetric encryption. [Figure 2] If Bob encrypts a message with Alice’s public key, only Alice’s private key can decrypt the message. This principle is what allows the SSH protocol to authenticate identity. If Alice (client) can decrypt Bob’s (server) message, then it proves Alice is in possession of the paired private key. This is, in theory, how SSH keys authentication should work. Unfortunately with the dynamic nature of infrastructure today, SSH keys are increasingly shared or managed improperly, compromising its integrity. To learn more, read this article, How to SSH Properly.

Listen to this article
Asymmetric Encryption Algorithms
What makes asymmetric encryption powerful is that a private key can be used to derive a paired public key, but not the other way around. This principle is core to public-key authentication. If Alice had used a weak encryption algorithm that could be brute-forced by today's processing capabilities, a third party could derive Alice's private key using her public key. Protecting against a threat like this requires careful selection of the right algorithm.
There are three classes of these algorithms commonly used for asymmetric encryption: RSA, DSA, and elliptic curve based algorithms. To properly evaluate the strength and integrity of each algorithm, it is necessary to understand the mathematics that constitutes the core of each algorithm.
RSA: Integer Factorization
First used in 1978, the RSA cryptography is based on the held belief that factoring large semi-prime numbers is difficult by nature. Given
that no general-purpose formula has been found to factor a compound number into its prime factors, there is a direct relationship between
the size of the factors chosen and the time required to compute the solution. In other words, given a number n=p\*q where
p and q are sufficiently large prime numbers, it can be assumed that anyone who can factor n into its
component parts is the only party that knows the values of p and q. The same logic exists for public and private
keys. In fact, p & q are necessary variables for the creation of a private key, and n is a variable for the subsequent public key. This presentation simplifies RSA integer factorization. For those interested in
learning more, click here.
DSA: Discrete Logarithm Problem & Modular Exponentiation
DSA follows a similar schema, as RSA with public/private keypairs that are mathematically related. What makes DSA different from RSA is that
DSA uses a different algorithm. It solves an entirely different problem using different elements, equations, and steps. While the discrete
log problem is fun, it is out of scope for this post. What is important to note is the use of
a randomly generated number, m, is used with signing a message along with a private key, k. This number m must be kept private. More
in this later.
ECDSA & EdDSA: Elliptic Curve Discrete Logarithm Problem
Algorithms using elliptic curves are also based on the assumption that there is no generally efficient solution to solving a discrete log problem. However, ECDSA/EdDSA and DSA differ in that DSA uses a mathematical operation known as modular exponentiation while ECDSA/EdDSA uses elliptic curves. The computational complexity of the discrete log problem allows both classes of algorithms to achieve the same level of security as RSA with significantly smaller keys.

Comparing Encryption Algorithms
Choosing the right algorithm depends on a few criteria:
- Implementation - Can the experts handle it, or does it need to be rolled?
- Compatibility - Are there SSH clients that do not support a method?
- Performance - How long will it take to generate a sufficiently secure key?
- Security - Can the public key be derived from the private key? (The use of quantum computing to break encryption is not discussed in this article.)
RSA
| Implementation | RSA libraries can be found for all major languages, including in-depth libraries (JS, Python, Go, Rust, C). |
|---|---|
| Compatibility | Usage of SHA-1 (OpenSSH) or public keys under 2048-bits may be unsupported. |
| Performance | Larger keys require more time to generate. |
| Security | Specialized algorithms like Quadratic Sieve and General Number Field Sieve exist to factor integers with specific qualities. |
Time has been RSA’s greatest ally and greatest enemy. First published in 1977, RSA has the widest support across all SSH clients and languages and has truly stood the test of time as a reliable key generation method. Subsequently, it has also been subject to Moore’s Law for decades and key bit-length has grown in size. According to NIST standards, achieving 128-bit security requires a key with length 3072 bits whereas other algorithms use smaller keys. Bit security measures the number of trials required to brute-force a key. 128 bit security means 2128 trials to break.
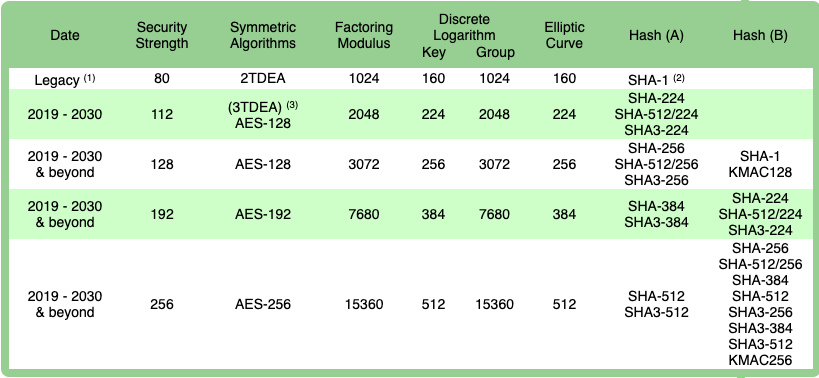

Figure 4 - NIST 2020 Recommendations for RSA key bit-length (Factoring Modulus)
DSA
| Implementation | DSA was adopted by FIPS-184 in 1994. It has ample representation in major crypto libraries, similar to RSA. |
|---|---|
| Compatibility | While DSA enjoys support for PuTTY-based clients, OpenSSH 7.0 disables DSA by default. |
| Performance | Significant improvement in key generation times to achieve comparable security strengths, though recommended bit-length is the same as RSA. |
| Security | DSA requires the use of a randomly generated unpredictable and secret value that, if discovered, can reveal the private key. |
Recall earlier in the article:
“What is important to note is the use of a randomly generated number, m, is used with signing a message along with a private key, k.
This number m must be kept privately.”
The value mis meant to be a nonce, which is a unique value included in many cryptographic protocols. However, the additional
conditions of unpredictability and secrecy makes the nonce more akin to a key, and therefore extremely important.
Not only is it difficult to ensure true randomness within a machine, but improper implementation can break encryption. For example:
-
Android’s Java
SecureRandomclass was known to create colliding R values. In other words, the class reused some randomly generated numbers. This exposed a number of different Android-based Bitcoin wallets to having their private keys stolen. The requirements of the noncemmeans that any two instances with the same nonce value could be reverse engineered and reveal the private key used to sign transactions. -
Taking this a step further, fail0verflow discovered the private key used to sign firmware updates for the Sony Playstation 3. In other words, programmers could write their own code, sign it with the revealed private key, and run it on the PS3. As it turns out, Sony was using the same random number to sign each message.
ECDSA & EdDSA
The two examples above are not entirely sincere. Both Sony and the Bitcoin protocol employ ECDSA, not DSA proper. ECDSA is an elliptic curve implementation of DSA. Functionally, where RSA and DSA require key lengths of 3072 bits to provide 128 bits of security, ECDSA can accomplish the same with only 256-bit keys. However, ECDSA relies on the same level of randomness as DSA, so the only gain is speed and length, not security.
In response to the desired speeds of elliptic curves and the undesired security risks, another class of curves has gained some notoriety. EdDSA solves the same discrete log problem as DSA/ECDSA, but uses a different family of elliptic curves known as the Edwards Curve (EdDSA uses a Twisted Edwards Curve). While offering slight advantages in speed over ECDSA, its popularity comes from an improvement in security. Instead of relying on a random number for the nonce value, EdDSA generates a nonce deterministically as a hash making it collision resistant.
Taking a step back, the use of elliptic curves does not automatically guarantee some level of security. Not all curves are the same. Only a few curves have made it past rigorous testing. Luckily, the PKI industry has slowly come to adopt Curve25519 in particular for EdDSA. Put together that makes the public-key signature algorithm, Ed25519.
| Implementation | EdDSA is fairly new Crypto++ and cryptlib do not currently support EdDSA. |
|---|---|
| Compatibility | Compatible with newer clients, Ed25519 has seen the largest adoption among the Edward Curves, though NIST also proposed Ed448 in their recent draft of SP 800-186. |
| Performance | Ed25519 is the fastest performing algorithm across all metrics. As with ECDSA, public keys are twice the length of the desired bit security. |
| Security | EdDSA provides the highest security level compared to key length. It also improves on the insecurities found in ECDSA. |
Teleport cybersecurity blog posts and tech news
Every other week we'll send a newsletter with the latest cybersecurity news and Teleport updates.
RSA vs. DSA vs. ECDSA vs. EdDSA
Below we list the common differences between RSA, DSA, ECDSA, and EdDSA algorithms:
| RSA | DSA | ECDSA | EdDSA | |
|---|---|---|---|---|
| Popularity | Most widely implemented and supported. | Its notorious security history makes it less popular. | Fairly new but not as popular as EdDSA. | Fairly new but favoured by most modern cryptographic libraries. |
| Performance | Larger keys require more time to generate. | Faster for signature generation but slower for validation. | Public keys are twice the length of the desired bit security. | EdDSA is the fastest performing algorithm across all metrics. |
| Security | Specialized algorithms like Quadratic Sieve and General Number Field Sieve exist to factor integers with specific qualities. | DSA requires the use of a randomly generated unpredictable and secret value that, if discovered, can reveal the private key. | Vulnerable if pseudo random number aren't cryptographically strong. | EdDSA provides the highest security level compared to key length. It also improves on the insecurities found in ECDSA. |
How to generate SSH keys with RSA, DSA, ECDSA, or EdDSA?
RSA is the default key type when generated using the ssh-keygen command. To generate SSH keys with given algorithm type, supply -t flag to ssh-keygen command. Below is an example of generating ed25519 key:
$ ssh-keygen -t ed25519 -C "unique name to identify this key."
Both public and private keys (ssh key pair) are generated with the above command. The private key never leave user's computer, and the public key is stored in the server's authorized_keys file.
The SSH key fingerprint can be checked with the following command:
$ ssh-keygen -l -f <key file>
For more details, learn how to generate SSH keys.
Conclusion
When it comes down to it, the choice is between RSA 2048/4096 and Ed25519 and the trade-off is between performance and compatibility. RSA is universally supported among SSH clients while EdDSA performs much faster and provides the same level of security with significantly smaller keys. Peter Ruppel puts the answer succinctly:
The short answer to this is: as long as the key strength is good enough for the foreseeable future, it doesn't really matter. Because here we are considering a signature for authentication within an SSH session. The cryptographic strength of the signature just needs to withstand the current, state-of-the-art attacks.
Just don’t use ECDSA/DSA!
Certificates better than keys
Although keys are a relatively secure authentication method for SSH when compared with password-based authentication, keys create an equal amount of operational and security overhead on the administration side. Key rotation and key invalidation remain a challenge that can be resolved using certificate-based authentication. Teleport offers SSH certificate-based access solution with additional benefits of audit logging, session recording, and RBAC for SSH. Teleport is open source and can be used as a drop replacement for OpenSSH servers. Learn why certificates are better than keys for SSH and get started with Teleport today -https://goteleport.com/docs/
Tags
Teleport Newsletter
Stay up-to-date with the newest Teleport releases by subscribing to our monthly updates.

Subscribe to our newsletter

